Spirit 使用说明
以下内容整理自“ https://spirit-docs.readthedocs.io/en/latest/index.html ”
Spirit框架概述
Spirit 是跨平台的原子级自旋模拟框架,具有以下核心特点:
支持GPU加速(CUDA)和CPU多核(OpenMP)并行计算
提供实时3D可视化桌面界面
以Python API用于复杂工作流
支持Windows/Linux/macOS全平台
核心功能
物理模拟能力
功能类别
具体实现
基础模型
海森堡模型(含DMI/偶极相互作用)
动力学模拟
LLG方程求解(SIB/Heun方法)
静态计算
能量最小化(VP/LBFGS求解器)
路径分析
GNEB方法计算能垒
技术特性对比
特性
CPU版本
GPU版本
并行加速
OpenMP多核
CUDA加速
典型性能
1M spins/s
10M spins/s
内存需求
中等
较高
适用场景
中小型系统
大规模系统
安装指南
(以下所有内容以python版本的spirit例)
Python包安装
Python包安装需要打开终端Shell,配置版本建议以python3.8到3.13之间,过高的版本可能会无法安装spirit
spirit-python的工作流程分为两部分:
1.在input.cfg文件中,依据需求整理好配置文件。
2.依据计算需要整理好Usage代码,使用python提交。
input.cfg文件
(具体内容见Spirit说明网页的Spirit_inputfile部分)
输入输出文件配置
这部分指定了计算得到的文件的存储位置以及存储文件名字,其中自上而下分别表示文件名以计算生成的时间命名,计算得到的日志文件log保存在根目录,其余计算文件保持在output文件夹中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 ############# Spirit Configuration ############## ### Output Folders output_file_tag <time> log_output_folder . llg_output_folder output mc_output_folder output gneb_output_folder output mmf_output_folder output ema_output_folder output ### Save input parameters on State creation/deletion save_input_initial 0 save_input_final 0 ### Save atom positions on State creation/deletion save_positions_initial 0 save_positions_final 0 ### Save exchange and DM neighbours on State creation/deletion save_neighbours_initial 0 save_neighbours_final 0
哈密顿量
该部分是微磁模拟过程中需要进行修改的主要部分。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 ### Hamiltonian Type (heisenberg_neighbours, heisenberg_pairs, gaussian) hamiltonian heisenberg_pairs n_interaction_pairs 3 i j da db dc Jij Dij Dijx Dijy Dijz 0 0 -1 1 0 10.0 3.0 0.000 1.0000 0.00 0 0 0 1 0 10.0 3.0 0.8660 0.5000 0.00 0 0 1 0 0 10.0 3.0 0.8660 -0.5000 0.00 ### Uniaxial anisotropy constant [meV] anisotropy_magnitude 0.0 anisotropy_normal 0.0 0.0 1.0 ### µSpin mu_s 1.5 ### Boundary_conditions (a b c): 0(open), 1(periodical) boundary_conditions 1 1 0 ### External magnetic field vector[T] external_field_magnitude 20 external_field_normal 0.0 0.0 0.0 ### Dipole-dipole interaction caclulation method ### (fft, fmm, cutoff, none) ddi_method none ### DDI number of periodic images in (a b c) ddi_n_periodic_images 4 4 4 ### DDI cutoff radius (if cutoff is used) ddi_radius 0.0 # If set to 1 zero padding is performed even for periodic directions, # if set to 0 it is skipped for peridodic directions (improves speed and memory footprint) ddi_pb_zero_padding 1 ################ End Hamiltonian #################
其中自上到下分别包括了:
1 2 ### Hamiltonian Type (heisenberg_neighbours, heisenberg_pairs, gaussian) hamiltonian heisenberg_pairs
spirit中包含了三种可选择的哈密顿量形式,即可海森堡最近邻交换、海森堡指定对交换、高斯哈密顿量。
1 2 3 4 5 6 n_interaction_pairs 3 i j da db dc Jij Dij Dijx Dijy Dijz 0 0 -1 1 0 10.0 3.0 0.000 1.0000 0.00 0 0 0 1 0 10.0 3.0 0.8660 0.5000 0.00 0 0 1 0 0 10.0 3.0 0.8660 -0.5000 0.00
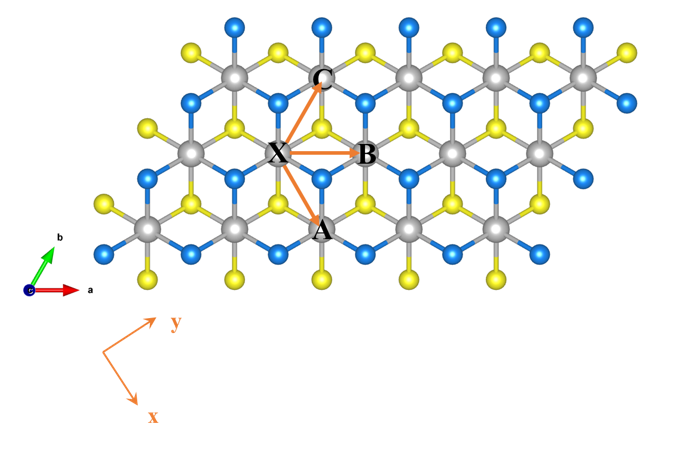
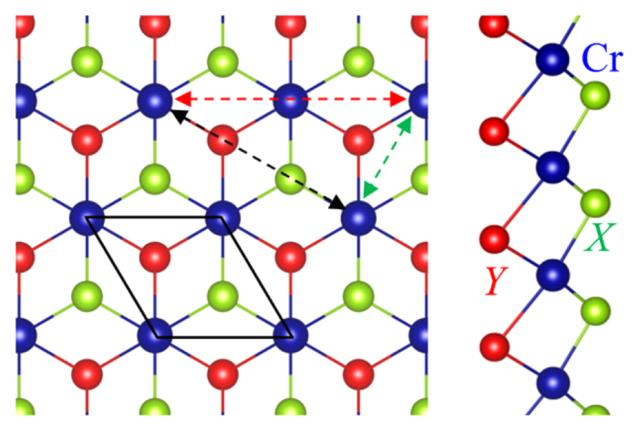
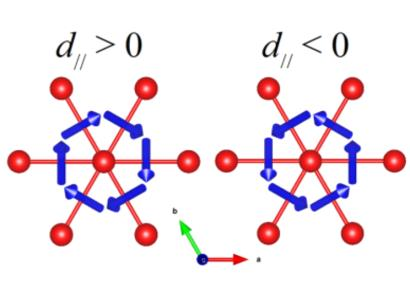
i j指定有几个不可约的指定对,上述例子为三对不可约的指定对。 其中,i表示在晶格中第几个原子,在spirit中,我们可以在一个布拉维格子中指定多个原子。j表示沿着对应的晶列方向的第几个晶格,而方向则由右侧的da_db_dc指定。da db dc的数值即spirit寻找与给定原子发生交换作用的原子的步长,da,db,dc即布拉维格子的基矢倍数。上面给的例子对应于六方晶系的三个指定对即如下所示:
图中,a、b是布拉维格子的基矢;x、y是实际空间的坐标矢量,用例中给的-1 1 0即是表征图中A位原子与X原子的相互作用对。
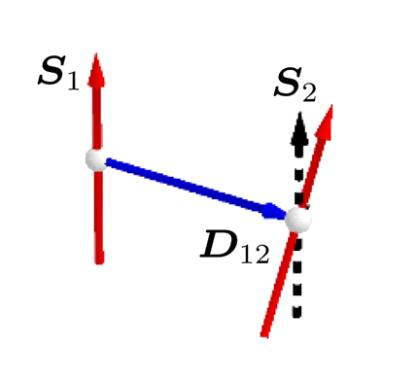
Jij Dij分别表示的是海森堡交换参数的强度和DM相互作用参数的强度,单位均为meV。Dijx Dijy Dijz表示的DM相互作用矢量的在实空间坐标系里的三个投影,0.00 1.00 0.00即表示DM矢量方向沿y方向。Dij决定,而方向只由Dijx Dijy Dijz决定,并且方向数组在spirit中是归一化(Normalization)处理的,这意味着输入0.00 1.00 0.00与输入0.00 5.00 0.00的结果是一样的。
spirit软件中的哈密顿量如下所示(PHYSICAL REVIEW B 99, 224414):
H = − ∑ i μ i B ⋅ n i − ∑ i ∑ j K j ( K ^ j ⋅ n i ) 2 − ∑ ⟨ i j ⟩ J i j n i ⋅ n j − ∑ ⟨ i j ⟩ D i j ⋅ ( n i × n j ) + 1 2 μ 0 4 π ∑ i , j i ≠ j μ i μ j ( n i ⋅ r ^ i j ) ( n j ⋅ r ^ i j ) − n i ⋅ n j r i j 3 (1) \begin{aligned}
\mathcal{H} = & -\sum_{i} \mu_i \mathbf{B} \cdot \mathbf{n}_i
- \sum_{i} \sum_{j} K_j (\hat{\mathbf{K}}_j \cdot \mathbf{n}_i)^2 \\
& -\sum_{\langle ij \rangle} J_{ij} \mathbf{n}_i \cdot \mathbf{n}_j
- \sum_{\langle ij \rangle} \mathbf{D}_{ij} \cdot (\mathbf{n}_i \times \mathbf{n}_j) \\
& + \frac{1}{2} \frac{\mu_0}{4\pi} \sum_{\substack{i,j \\ i\neq j}} \mu_i \mu_j \frac{(\mathbf{n}_i \cdot \hat{\mathbf{r}}_{ij}) (\mathbf{n}_j \cdot \hat{\mathbf{r}}_{ij}) - \mathbf{n}_i \cdot \mathbf{n}_j}{r_{ij}^3} \tag{1}
\end{aligned}
H = − i ∑ μ i B ⋅ n i − i ∑ j ∑ K j ( K ^ j ⋅ n i ) 2 − ⟨ ij ⟩ ∑ J ij n i ⋅ n j − ⟨ ij ⟩ ∑ D ij ⋅ ( n i × n j ) + 2 1 4 π μ 0 i , j i = j ∑ μ i μ j r ij 3 ( n i ⋅ r ^ ij ) ( n j ⋅ r ^ ij ) − n i ⋅ n j ( 1 )
自上而下,各项依次为:
相较于繁琐的指定对模式,spirit中还提供了另外一类设定Jij与Dij的模式,即近邻壳(Neighbour shells)方法。
1 2 3 4 5 6 7 8 9 10 11 12 13 ### Hamiltonian Type (heisenberg_neighbours, heisenberg_pairs, gaussian) hamiltonian heisenberg_neighbours ### Exchange: number of shells and constants [meV / unique pair] n_shells_exchange 3 jij 10.0 3.0 1.0 ### Chirality of DM vectors (+/-1=bloch, +/-2=neel) dm_chirality 2 ### DMI: number of shells and constants [meV / unique pair] n_shells_dmi 2 dij 6.0 0.5
在哈密顿量模式中选择heisenberg_neighbours,对于海森堡交换相互作用,设置n_shells_exchange 3表示了考虑最近邻、次近邻、次次近邻三层。jij 10.0 3.0 1.0定义。
DM相互作用的描述也是类似的,n_shells_dmi 2表示了考虑最近邻和次近邻两层的DM相互作用,其DM作用强度由dij 6.0 0.5定义。
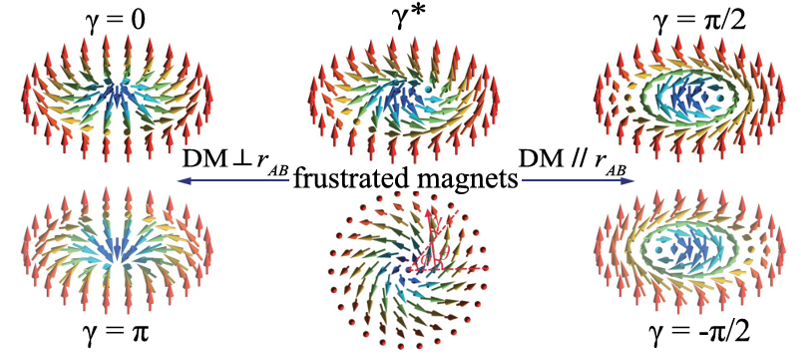
由于DM相互作用的形式是具备矢量性质的,在使用heisenberg_neighbours方法时,我们对于DM向量的手性,是不能通过手动来调节的,而是在Bloch和Neel两种DM矢量中选择一个,这两种DMI矢量决定了最后skyrmion的构型。
需要注意的是,对于Kz>0,即面外铁磁作为基态的体系来说,我们通常可以通过时钟法计算DM在x-y平面上的分量,这个分量的大小和方向都是可以确定的。
哈密顿量中所有的相互作用参数都是自带负号的,在进行微磁模拟时应当注意。
②单离子各向异性的设置如下,其中anisotropy_magnitude表示其大小,anisotropy_normal表示了易磁化轴的方向。在一般的二维材料微磁学模拟中,我们一般设置易磁化轴为z轴,表示其磁矩倾向于垂直面外排列。
1 2 3 ### Uniaxial anisotropy constant [meV] anisotropy_magnitude 0.0 anisotropy_normal 0.0 0.0 1.0
③赛曼项的设置如下,其中µSpin表示磁矩的大小,单位为玻尔磁子μB,External magnetic field vector为外磁场,其中external_field_magnitude表示外加磁场的大小,external_field_normal表示了外加磁场的方向。boundary_conditions可以针对边界情况选择开放边界或者周期性边界。
1 2 3 4 5 6 7 8 9 ### µSpin mu_s 1.5 ### Boundary_conditions (a b c): 0(open), 1(periodical) boundary_conditions 1 1 0 ### External magnetic field vector[T] external_field_magnitude 20 external_field_normal 0.0 0.0 0.0
④磁偶极偶极相互作用的设置如下
1 2 3 4 5 6 7 8 9 10 11 12 13 ### Dipole-dipole interaction caclulation method ### (fft, fmm, cutoff, none) ddi_method none ### DDI number of periodic images in (a b c) ddi_n_periodic_images 4 4 4 ### DDI cutoff radius (if cutoff is used) ddi_radius 0.0 # If set to 1 zero padding is performed even for periodic directions, # if set to 0 it is skipped for peridodic directions (improves speed and memory footprint) ddi_pb_zero_padding 1
其中ddi_method 可以选择不同的算法对偶极偶极相互作用进行处理。
1 2 3 4 `none` - 不考虑偶极偶极相互作用 `fft` - 采用快速傅里叶变换处理 `cutoff` - 采用一个截断半径处理,需要额外指定半径大小 'ddi_radius' `fmm` - Uses the Fast-Multipole-Method
需要指出的是,对于磁性体系偶极偶极相互作用的强度一般比其他相互作用要弱上两到三个数量级,一般在无特殊情况下,选择none模式不对其进行考虑即可。
晶体构型
决定了计算过程中的原子间几何结构
1 2 3 4 5 6 7 8 9 10 11 ################### Geometry ##################### ### Lattice constant for basis and translations lattice_constant 1.0 ### The bravais lattice type bravais_lattice HEX2D ### Number of basis cells along principal ### directions (a b c) n_basis_cells 120 120 1 ################# End Geometry ###################
其中晶格常数对于磁偶极偶极相互作用有影响。
1 2 ### Lattice constant for basis and translations lattice_constant 1.0
布拉维格子类型,此处设置的类型为二维六方的晶胞bravais_lattice HEX2D,在spirit中,可以设置多种类型的晶胞,如下图所示:
Bravais Lattice Type
Keyword
Comment
Simple cubic
sc
Body-centered cubic
bcc
Face-centered cubic
fcc
Hexagonal (2D)
hex2d
60deg angle
Hexagonal (2D)
hex2d60
60deg angle
Hexagonal (2D)
hex2d120
120deg angle
此外,还可以之间在实空间中指定布拉维基矢来直接描述晶胞,即:
1 2 3 4 5 6 7 8 ### bravais_vectors or bravais_matrix ### a.x a.y a.z a.x b.x c.x ### b.x b.y b.z a.y b.y c.y ### c.x c.y c.z a.z b.z c.z bravais_vectors 1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0
最后是设置的计算尺度的大小,如下例即沿a与b的基矢方向取120*120的超胞。
1 2 3 ### Number of basis cells along principal ### directions (a b c) n_basis_cells 120 120 1
LLG方程参数设置
spirit的微磁学模拟中,微磁动力学于静态微磁均可以通过LLG方程实现,以下是spirit中LLG方程的形式:
∂ n i ∂ t = − γ ( 1 + α 2 ) μ i n i × B i eff − γ α ( 1 + α 2 ) μ i n i × ( n i × B i eff ) − α − β ( 1 + α 2 ) u n i × ( J ^ e ⋅ ∇ r ) n i + 1 + β α ( 1 + α 2 ) u n i × [ n i × ( J ^ e ⋅ ∇ r ) n i ] , \begin{aligned}
\frac{\partial n_i}{\partial t} = & -\frac{\gamma}{(1 + \alpha^2)\mu_i}n_i \times B_i^{\text{eff}} \\
& -\frac{\gamma\alpha}{(1 + \alpha^2)\mu_i}n_i \times (n_i \times B_i^{\text{eff}}) \\
& -\frac{\alpha - \beta}{(1 + \alpha^2)}u\,n_i \times (\hat{J}_e \cdot \nabla_r)n_i \\
& +\frac{1 + \beta\alpha}{(1 + \alpha^2)}u\,n_i \times \left[n_i \times (\hat{J}_e \cdot \nabla_r)n_i\right],
\end{aligned}
∂ t ∂ n i = − ( 1 + α 2 ) μ i γ n i × B i eff − ( 1 + α 2 ) μ i γ α n i × ( n i × B i eff ) − ( 1 + α 2 ) α − β u n i × ( J ^ e ⋅ ∇ r ) n i + ( 1 + α 2 ) 1 + β α u n i × [ n i × ( J ^ e ⋅ ∇ r ) n i ] ,
主变量
n i n_i n i ∣ n i ∣ = 1 |n_i| = 1 ∣ n i ∣ = 1 ∂ n i ∂ t \frac{\partial n_i}{\partial t} ∂ t ∂ n i
参数
γ \gamma γ rad ⋅ s − 1 ⋅ T − 1 \text{rad} \cdot \text{s}^{-1} \cdot \text{T}^{-1} rad ⋅ s − 1 ⋅ T − 1 α \alpha α μ i \mu_i μ i A ⋅ m 2 \text{A} \cdot \text{m}^2 A ⋅ m 2 B i eff B_i^{\text{eff}} B i eff T \text{T} T β \beta β u u u u = j e P g μ B 2 e M S u = \frac{j_e P g \mu_B}{2 e M_S} u = 2 e M S j e P g μ B j e j_e j e P P P g g g e e e M S M_S M S J ^ e \hat{J}_e J ^ e ∇ r = ∂ / ∂ r \nabla_r = \partial/\partial r ∇ r = ∂ / ∂ r
在进行静态微磁模拟时,通常仅考虑 LLG 方程的前两项:
∂ n i ∂ t = − γ ( 1 + α 2 ) μ i n i × B i eff − γ α ( 1 + α 2 ) μ i n i × ( n i × B i eff ) \frac{\partial n_i}{\partial t} = -\frac{\gamma}{(1 + \alpha^2)\mu_i}n_i \times B_i^{\text{eff}} - \frac{\gamma\alpha}{(1 + \alpha^2)\mu_i}n_i \times \left(n_i \times B_i^{\text{eff}}\right)
∂ t ∂ n i = − ( 1 + α 2 ) μ i γ n i × B i eff − ( 1 + α 2 ) μ i γ α n i × ( n i × B i eff )
其中,有效磁场由哈密顿量对自旋方向的变分给出:
B i eff = − ∂ H ∂ n i B_i^{\text{eff}} = -\frac{\partial H}{\partial n_i}
B i eff = − ∂ n i ∂ H
其中 H H H B i eff B_i^{\text{eff}} B i eff
在实际的计算中,严格实现 B i eff = 0 B_i^{\text{eff}} = 0 B i eff = 0 ∣ B i eff ∣ < ϵ |B_i^{\text{eff}}| < \epsilon ∣ B i eff ∣ < ϵ γ \gamma γ α \alpha α μ i \mu_i μ i B m i n eff B_{min}^{\text{eff}} B min eff
也就是下列的LLG参数部分的:
1 2 ### Force convergence parameter llg_force_convergence 10e-7
在此处即可设置最小的收敛精度,一般来说精度在10e-5即可得到较为稳定的磁拓扑形貌。
以下是LLG参数部分的所有可调的内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 ################ LLG Parameters ################## ### Maximum wall time for single simulation ### hh:mm:ss, where 0:0:0 is infinity llg_max_walltime 0:0:0 ### Seed for Random Number Generator llg_seed 20016 ### Number of iterations llg_n_iterations 100000 ### Number of iterations after which to save llg_n_iterations_log 2000 ### Number of iterations that gets run with no checks or outputs (Increasing this boosts performance, especially in CUDA builds) llg_n_iterations_amortize 1 ### Temperature [K] llg_temperature 0 llg_temperature_gradient_direction 1 0 0 llg_temperature_gradient_inclination 0 ### Damping [none] llg_damping 0.3 ### Non-adiabatic damping llg_beta 0.1 ### Time step dt llg_dt 1.0E-3 ### Bools 0 = false || 1 = true llg_renorm 1 ### 0 = use the pinned monolayer approximation ### 1 = use the gradient approximation llg_stt_use_gradient 1 ### Spin transfer torque parameter proportional ### to injected current density llg_stt_magnitude 1.0 ### Spin current polarisation normal vector llg_stt_polarisation_normal 1.0 0.0 0.0 ### Force convergence parameter llg_force_convergence 10e-7 ### Output configuration llg_output_any 1 llg_output_initial 1 llg_output_final 1 llg_output_energy_step 0 llg_output_energy_archive 1 llg_output_energy_spin_resolved 0 llg_output_energy_divide_by_nspins 1 llg_output_energy_add_readability_lines 1 llg_output_configuration_step 1 llg_output_configuration_archive 0 llg_output_configuration_filetype 3 ############## End LLG Parameters ################
对于微磁模拟,我们可以设置其中的部分参数,如下中的llg_damping即对应了吉尔伯特阻尼系数(Gilbert damping parameter),而llg_beta对应的是自旋转移力矩(Spin-transfer torque)的阻尼系数。
需要指出的是,对于不同体系的微磁模拟,llg_dt是一个需要注意的量,这个数值决定了模拟的微分方程步长,如果模拟反铁磁体系,可能会因为时间步长过小导致体系一直无法有效收敛。
具体的关于llg_dt的测试可以查阅spirit软件包的的PRB文章。
1 2 3 4 5 6 7 ### Damping [none] llg_damping 0.3 ### Non-adiabatic damping llg_beta 0.1 ### Time step dt llg_dt 1.0E-3
如果需要进行有限温的模拟,则需在有效场中增加温度相关的高斯噪声项,即 B i → B i + B i t h B_i \to B_i + B_i^{th} B i → B i + B i t h
B i t h ( t ) = 2 D i η i ( t ) = 2 α k B T μ i γ η i ( t ) B_i^{th}(t) = \sqrt{2D_i} \eta_i(t) = \sqrt{2\alpha k_B T \frac{\mu_i}{\gamma}} \eta_i(t)
B i t h ( t ) = 2 D i η i ( t ) = 2 α k B T γ μ i η i ( t )
其中噪声幅值由涨落-耗散定理确定,η i \eta_i η i
⟨ B i α t h ( t ) ⟩ = 0 \langle B_{i\alpha}^{th}(t) \rangle = 0
⟨ B i α t h ( t )⟩ = 0
方差满足关联关系
⟨ B i α t h ( t ) B j β t h ( 0 ) ⟩ = 2 D i δ i j δ α β δ ( t ) \langle B_{i\alpha}^{th}(t) B_{j\beta}^{th}(0) \rangle = 2D_i \delta_{ij} \delta_{\alpha \beta} \delta(t)
⟨ B i α t h ( t ) B j β t h ( 0 )⟩ = 2 D i δ ij δ α β δ ( t )
在数值实现中,每个时间步的噪声向量 η i ( t ) \eta_i(t) η i ( t ) 1 / δ t 1/\sqrt{\delta t} 1/ δ t
如下llg_temperature是温度的具体值,单位为开尔文。
1 2 3 4 5 6 7 8 ### Damping [none] llg_damping 0.3 ### Non-adiabatic damping llg_beta 0.1 ### Time step dt llg_dt 1.0E-3
对于外加电流驱动下的磁行为,可以采用spirit自带的自旋转移力矩(Spin Transfer Torque,STT)模块进行模拟。
可以在llg_stt_use_gradient部分选择两种模式。
(1) 钉扎单层近似(0 = pinned monolayer approximation)
T STT ∝ ( u ⋅ ∇ ) m − β m × ( u ⋅ ∇ ) m \text{T}_{\text{STT}} \propto (u \cdot \nabla)m - \beta m \times (u \cdot \nabla)m
T STT ∝ ( u ⋅ ∇ ) m − β m × ( u ⋅ ∇ ) m
(u u u
某一磁性单层(如钉扎层)的磁化方向被固定,不随电流或外场变化。
(2) 梯度近似(1 = gradient approximation)
T STT ∝ m × ( m ⋅ ∇ ) m − β m × [ m × ( m ⋅ ∇ ) m ] \text{T}_{\text{STT}} \propto m \times (m \cdot \nabla)m - \beta m \times \left[m \times (m \cdot \nabla)m\right]
T STT ∝ m × ( m ⋅ ∇ ) m − β m × [ m × ( m ⋅ ∇ ) m ]
自旋极化电流的极化方向与磁化强度的空间梯度相关(如 m×(m⋅∇)m\mathbf{m} \times (\mathbf{m} \cdot \nabla)\mathbf{m}m×(m⋅∇)m)。
特性 钉扎单层近似
梯度近似
磁化动态 忽略钉扎层动力学
显式包含磁化梯度效应
空间分辨率需求 较低(仅需分辨主体磁化变化)
较高(需分辨梯度变化区域)
计算资源 节省内存与计算时间
资源密集(尤其对大规模体系)
典型应用 自旋阀、磁隧道结的宏观电流响应
磁畴壁运动、涡旋态动力学
物理效应捕捉 忽略钉扎层与自由层的耦合细节
精确描述梯度驱动的非平衡效应
类似的,自旋极化电流的强度和方向分别由llg_stt_magnitude和llg_stt_polarisation_normal来定义。
1 2 3 4 5 6 7 8 ### 0 = use the pinned monolayer approximation ### 1 = use the gradient approximation llg_stt_use_gradient 1 ### Spin transfer torque parameter proportional ### to injected current density llg_stt_magnitude 1.0 ### Spin current polarisation normal vector llg_stt_polarisation_normal 1.0 0.0 0.0
Usage 使用说明
在spirit的python-API文档中给了三种用例,即能量最小化方法(Energy minimisation),LLG微磁动力学演化方法(LLG method),以及用于寻找不同磁态间过渡势垒的GNEB方法(GNEB method)。
以下以LLG方程为例,介绍几种用法。
①基础版本,从随机态开始演化
以input.cfg文件作为配置,采用LLG方法模拟simulation.METHOD_LLG,选择速度投影算法simulation.SOLVER_DEPONDT。
1 2 3 4 from spirit import simulation, state with state.State("input/input.cfg") as p_state: simulation.start(p_state, simulation.METHOD_LLG, simulation.SOLVER_DEPONDT)
②设定初始skyrmion配置的方法
在spirit中调用configuration模块,按照顺序设定初始磁构型为向上configuration.plus_z(p_state, idx_image=0)。configuration.skyrmion(p_state, 5.0,pos=[0,0,0], phase=-90.0, idx_image=0),设定尺寸为5个晶格常数,位置坐标为[0,0,0],skyrmion的相位角度为phase=-90.0
1 2 3 4 5 from spirit import state, configuration, simulation with state.State("input/input.cfg") as p_state: configuration.plus_z(p_state, idx_image=0) configuration.skyrmion(p_state, 5.0,pos=[0,0,0], phase=-90.0, idx_image=0) simulation.start(p_state, simulation.METHOD_LLG, simulation.SOLVER_DEPONDT, idx_image=0)
③设定初始磁构型配置为已有矢量场文件配置(OVF)的方法
在spirit中调用io模块,使用io.image_read读取已有的OVF文件,读取路径为主文件夹下的绝对路径。
1 2 3 4 from spirit import state, configuration, simulation, io with state.State("input/input07.cfg") as p_state: io.image_read(p_state, "output/2025-05-07_16-17-06_Image-00_Spins_08112.ovf", idx_image_infile=0, idx_image_inchain=-1, idx_chain=-1) simulation.start(p_state, simulation.METHOD_LLG, simulation.SOLVER_DEPONDT, idx_image=0)